DRA de polarización cilíndrica circular 3D utilizando una hélice dieléctrica parásita

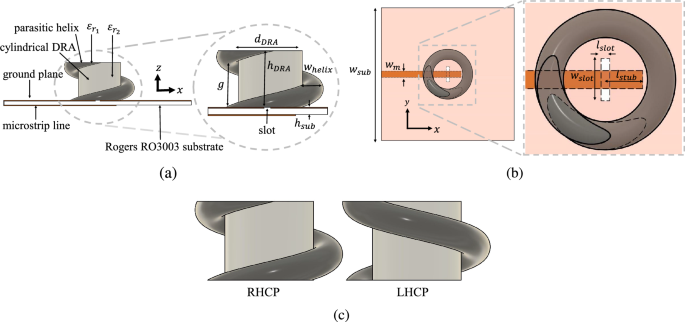
Propuesta de CDRA con estructura de alimentación por tornillo. (a) Visión lateral (B(vista superior)C) Estructura helicoidal dieléctrica de LHCP y RHCP.

La antena propuesta se muestra en la Fig. 1. Consta de dos estructuras dieléctricas: una antena resonadora cilíndrica dieléctrica (CDRA) y una espiral parásita dieléctrica colocada alrededor de la CDRA. Primero, las dimensiones del CDRA se modelan para la frecuencia resonante \(f_0\) A 5,8 GHz emocionante HEM\(_{11\Delta}\) situación^{14, 15}utilizando alimentación por ranura de acoplamiento⁷ establecido por la Ec. (1):

dónde C es la velocidad de la luz, \(r_{DRA}\) es el radio de la DRA (\(d_{DRA}/2\)) Y \(h_{DRA}\) Altura DR. El factor de forma específico de DRA da dimensión de radio \(r_{DRA}=9\) mm y altura \(h_{DRA}=16\) mm, utilizando un material con permitividad relativa \(\varepsilon _{r2}=9\). En la Figura 2, la simulación \(|S_{11}|\) del CDRA diseñado, y el patrón de radiación simulado de ambos planos a 5,8 GHz. Podemos ver que CDRA tiene una ganancia máxima de alrededor de 6dB, mientras que coincide bien con la frecuencia de diseño.

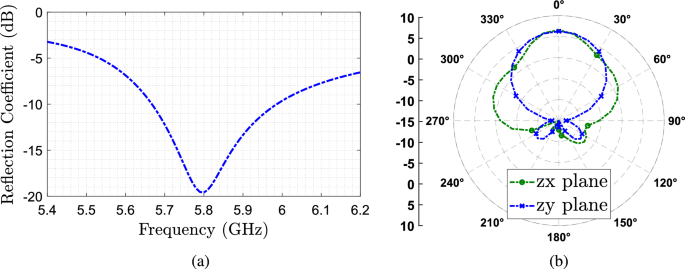
Resultados de la simulación CDRA. (a) \(S_{11}\) en función de la frecuencia (B) patrón de radiación a 5,8 GHz.

Una vez que el CDRA está correctamente diseñado, pasamos a implementar la hélice dieléctrica que le dará polarización circular al DRA original. Primero, las ecuaciones de la curva espiral se definen en función de los parámetros que se muestran en la Fig. 1. Y las ecuaciones con un plano de referencia cartesiano (XY yY z)^dieciséis Se muestra para cada eje en las ecuaciones. (2), (3) y (4):

dónde \(w_{hélice}/2\) es el radio de la espiral, gramo Especifica la distancia total o espacio entre cada vuelta, mientras que la longitud total de la hélice está determinada por Rque comienza desde \(t_0 = 0\) a \(t_f=2\pi h_{dra}/{g}\)que depende de la altura del DRA \(h_{dra}\) y separación de roles. Para el diseño en espiral se realiza un estudio paramétrico con el fin de obtener una antena polarizada circularmente a 5.8 GHz. Este estudio incluye tres posibles parámetros de diseño para la hélice: anchura de la hélice \(w_{hélice}\)la permitividad relativa de la hélice \(\varepsilon _{r1}\)y el espacio entre vueltas gramo, que se puede obtener mediante el paso de la espiral. En cuanto a la permitividad de la bobina, se identificaron dos posibles casos de estudio: una permitividad superior a CDRA (\(\varepsilon _{r_1}\) = 13) y use el mismo valor de CDRA (\(\varepsilon _{r_1}\) = 9).

En la Figura 3 se muestran los resultados del estudio paramétrico utilizando diferentes valores del ancho del tornillo y su efecto sobre el coeficiente de reflectancia y la relación axial. Este estudio se realizó considerando las dos tolerancias relativas descritas anteriormente, 13 y 9, y un espacio helicoidal de 18 mm. Puede verse que en todos los casos la antena permanece idéntica a la frecuencia de interés, sin embargo, se produce un cambio de frecuencia y un deterioro de la relación axial cuando se reducen la permitividad relativa y el ancho de la bobina. Un segundo estudio de la variación del espacio entre giros gramo Se realiza fijando el ancho de la hélice en 3 mm. A partir de los resultados que se muestran en la Fig. 4, podemos ver que cuando se fija la permitividad, una mayor separación entre espiras conduce a un mayor ancho de banda AR. De estos estudios, en conclusión, necesitamos utilizar un mayor valor de permitividad de la hélice, y una mayor separación entre espiras, teniendo en cuenta el ancho de la hélice.

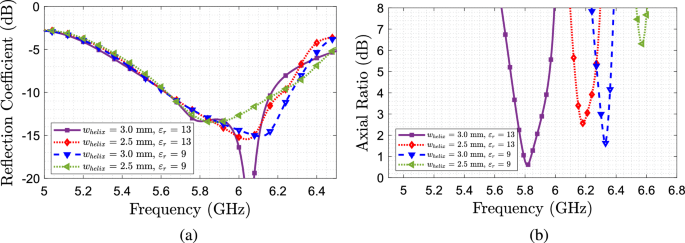
Un estudio paramétrico que tiene en cuenta diferentes anchos de hélice. (a) relación de pivote. (B) \(S_{11}\).

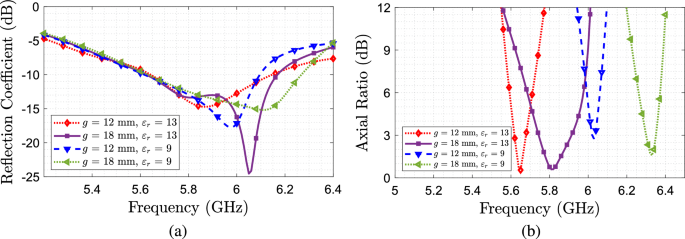
Un estudio paramétrico que tiene en cuenta los diferentes pasos de la espiral. (a) Arkansas(B) \(S_{11}\).

Resultados de simulación CDRA con un caracol parasitoide

La antena propuesta siguiendo el modelo mostrado en la Figura 1 tiene las siguientes dimensiones: \(d_{DRA}=18\) milímetro, \(h_{DRA}=16\) milímetro, \(\varepsilon _{r2}=9\)Y \(d_{hélice} = 18\) milímetro, \(w_{hélice} = 6.0\) milímetro \(g = 18\) mmf \(\varepsilon _{r1}=13\). Rogers Nutrición RO 3003 (\(\varepsilon _r = 3\) y bronceado\(\delta = 0.0013\)) sustrato utilizado. Dimensiones laterales y ancho del sustrato, como se muestra en la Figura 1 \(w_{sub}=80\) mmf \(h_{sub}=1.52\) mm, mientras que las dimensiones del orificio en el orificio de alimentación son \(w_{apertura}=9.0\) milímetro, \(l_{apertura}=1.8\) milímetro, \(l_{talón}=8\) mm y el ancho de la línea microstrip \(w_m=3.82\) milímetro. Se simularon dos implementaciones, la arquitectura RHCP y la arquitectura LHCP, utilizando ANSYS HFSS.

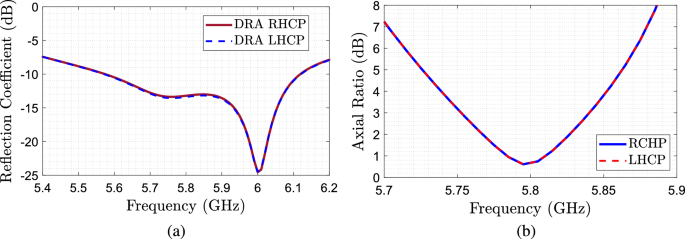
Resultados de simulación de antena. (a) \(S_{11}\) en función de la frecuencia CDRA con hélices. (B) Relación axial de los casos RHCP y LHCP.

En la Fig. 5 los coeficientes de reflexión simulados \(S_{11}\) de CDRA con hélice parasitoide y se muestran las relaciones axiales correspondientes. Podemos ver que cuando la hélice está presente, podemos ver claramente dos resonancias, que corresponden a los dos modos ortogonales excitados.^{17, 18}, resonando a 5,7 GHz y 6,1 GHz. En cuanto a las relaciones axiales, como era de esperar, ambas antenas tienen la misma relación axial, independientemente de la polarización, alcanzando valores inferiores a 3 dB en la frecuencia operativa.

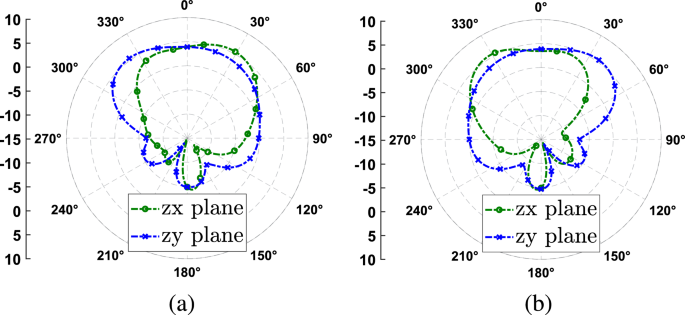
Modelo de radiación de ganancia simulada a 5,8 GHz en los dos planos principales y en los estados de polarización. (a) Antena RHCP. (B) Antena LHCP.

En la Fig. 6 se muestran los diagramas de radiación de ganancia simulada a 5,8 GHz para ambas polarizaciones. Podemos ver que la radiación de la antena se modifica ligeramente dependiendo de la polarización, por lo que la ganancia máxima es de 5 dB a la frecuencia de diseño en \(0^\círculo\). Finalmente, la Fig. 7 muestra la ganancia máxima simulada y la eficiencia de la antena sobre el ancho de banda de relación axial de la antena. Podemos ver que la eficiencia de la antena es aproximadamente el 80% del ancho de banda estimado, mientras que la ganancia máxima está entre 6 y 7 dBi en el mismo rango.

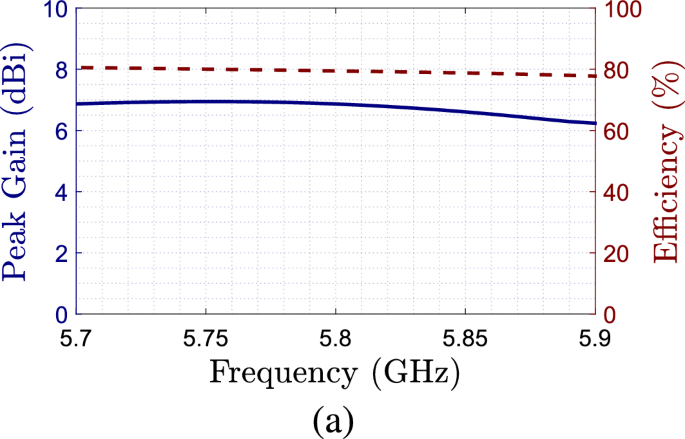
Ganancia y eficiencia máxima de la simulación en función de la frecuencia.

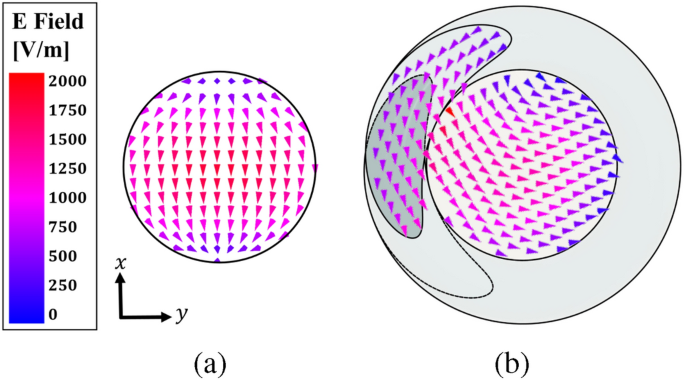
Distribución vectorial para simulación de campos electrónicos. (a) sidra. (B) CDRA con el caracol aislante parásito RHCP.

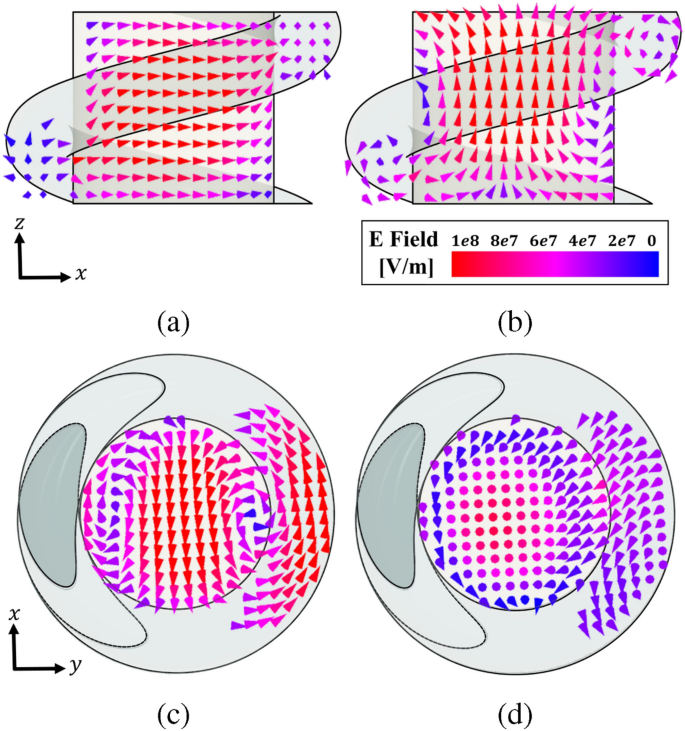
Distribución de vector de campo electrónico simulado en las frecuencias resonantes relevantes. (a(vista lateral a 5,76 GHz)B(vista lateral a 6,0 GHz), (C(vista superior a 5,76 GHz), (Dr) pantalla superior a 6,0 GHz.

Es importante identificar los modos creados en el CDRA con la hélice del búfer y verificar su ortogonalidad. La figura 8 muestra la distribución del vector de campo de electrones obtenida usando la simulación de onda completa. Y en CDRA sin la hélice, se espera el HEM\(_{11}\) La situación se ve claramente, mientras que cuando la hélice está presente, el campo eléctrico sigue el comportamiento de RHCP. Para ver e identificar estos dos modos ortogonales, se simula un DRA en una solución Eigenmode Ansys HFSS para obtener los campos en cada modo resonante. El primer modo está excitado a 5,76 GHz, como se muestra en la Figura 9, donde podemos identificarlo como HEM\(_{12\delta}\). El segundo modo se excita a 6,02 GHz, correspondiente a TM\(_{01\delta}\) modo, siendo ambos modos ortogonales¹⁹. Con base en este análisis, esperamos obtener una relación focal baja en la frecuencia de diseño \(f_0=5.8\) GHz, similar a lo que se logró al diseñar antenas parche polarizadas circularmente (CP) por excitación de modos ortogonales.